NCERT Solutions for Class 10 Maths Chapter 2 – Polynomials
Chapter with full detail information
https://brainytrainy0183.blogspot.com gives you detail information regarding chapter. Here we provide you each topic with full detail ( with definitions, and examples). In this , you will get definitions of each topic with detail examples and exercises 2.1 , 2.2 , 2.3 , and 2.4 (optional) solved. You can also comment us any further query.
Let’s start:
Polynomials
What is polynomial: An algebraic expression p(x) is in the form of p(x)=a0+a1x+a2x2+………+anxn , where the all a’s are real numbers (sometimes called the coefficients of the polynomials) and all indices of x are non-negative integers, is called a polynomial in x.
Note: A polynomial in x is said to be in standard form when the terms are written either in increasing order or decreasing order of the indices of x in various terms.
Degree of polynomial: If the p(x) is a polynomial in x , the highest power of x in p(x) is called the degree of polynomial. For example: 5x-4 is a polynomial in the variable x of degree 1 , 4x2+3x+2 is a polynomial in the variable x of degree 2 .
Note: Expressions like 1/x-1 , √x+5 , etc. are not polynomials.
Different types of polynomials:
1) Linear polynomial: A polynomial of highest degree 1 is called linear polynomial. It is in the form ax+b , where a,b are real numbers and a is non zero. For example: 4x-7 , 9x +4 , etc.
2) Quadratic polynomial: A polynomial of highest degree 2 is called quadratic polynomial. It is in the form ax2+bx+c , where a,b,c are real numbers and a is non- zero. For example: 2x2+5x-2=0 , 4x2+7x+4=0,etc.
3) Cubic polynomial: A polynomial of highest degree 3 is called cubic polynomial. It is in the form of ax3+bx2+cx+d , where a,b,c,d are real numbers and a is non- zero. For example: 4x3+3x2+5x+7=0 etc.
Zero of a polynomial: A real number k is called a zero of a polynomial p(x) , if p(k)=0.
i.e., a zero of a polynomial is the value of the variable for which the value of the polynomial becomes zero.
For example: 5x -10 = 0 or 5x=10 or x=2 , here we find value of x is 2 , so 2 is the zero of polynomial.
Note: A polynomial of degree n can have at the most n zeroes . So, a quadratic polynomial can have at the most 2 zeroes and a cubic polynomial can have at the most 3 zeroes.
How we locate Zeroes of a polynomial in graphically representation: The zeroes of a polynomial p(x) are precisely the x-coordinates of the points where the graph of y=p(x) intersects the x-axis.
Here, the graph cuts x-axis at two distinct points i.e A and A’ . Therefore, we say that above graph have two zeroes .
OR
The number of zeroes is 2 as the graph intersects the x-axis at two points.
Relationship between Zeroes and coefficients of a polynomial:
Sum of zeroes = α+β= -b/a= -( coefficient of x)/ coefficient of x2
Product of zeroes = αβ= c/a= constant term/coefficient of x2
Let’s say that α, βand γ are the zeroes of a cubic polynomial ax3+bx2+cx+d=0 , then
Sum of zeroes = α+β+ γ = -b/a = -(coefficient of x2)/coefficient of x3
Sum and product of zeroes = αβ+ β γ+ γ α = c/a = coefficient of x / coefficient of x3
Product of zeroes = αβ γ = -d/a = -(constant term)/ coefficient of x3
Division Algorithm for polynomials: The division algorithm states that given any polynomial p(x) and any non-zero polynomial g(x), there are polynomials q(x) and r(x) such that
P(x) = g(x)q(x) + r(x), where r(x) = 0 or degree r(x) <degree q(x).
Exercise 2.1
Question 1.)
Solution:
i. The number of zeroes is 0 the graph line is above x-axis and does not intersect the x- axis.
ii. The number of zeroes is one as the graph intersects the x-axis at one point only.
iii. The number of zeroes is three as the graph intersects the x-axis at three points .
iv. The number of zeroes is two as the graph intersects the x-axis at two points .
v. The number of zeroes is four as the graph intersects the
x-axis at four points.
vi. The number of zeroes is three as the graph intersects the x-axis at three points.
Exercise 2.2
Question 1.) Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.
Solutions:
(i)x2–2x –8
⇒x2– 4x+2x–8 = x(x–4)+2(x–4) = (x-4)(x+2)
Therefore, zeroes of polynomial equation x2–2x–8 are (4, -2)
Relationship:
Sum of zeroes = 4–2 = 2 = -(-2)/1 = -(Coefficient of x)/(Coefficient of x2)
Product of zeroes = 4×(-2) = -8 =-(8)/1 = (Constant term)/(Coefficient of x2)
(ii)4s2–4s+1
⇒4s2–2s–2s+1 = 2s(2s–1)–1(2s-1) = (2s–1)(2s–1)
Therefore, zeroes of polynomial equation 4s2–4s+1 are (1/2, 1/2)
Sum of zeroes = (½)+(1/2) = 1 = -4/4 = -(Coefficient of s)/(Coefficient of s2)
Product of zeros = (1/2)×(1/2) = 1/4 = (Constant term)/(Coefficient of s2 )
(iii) 6x2–3–7x
⇒6x2–7x–3 = (3x+1)(2x-3)
Therefore, zeroes of polynomial equation 6x2–3–7x are (-1/3, 3/2)
Sum of zeroes = -(1/3)+(3/2) = (7/6) = -(Coefficient of x)/(Coefficient of x2)
Product of zeroes = -(1/3)×(3/2) = -(3/6) = (Constant term) /(Coefficient of x2)
(iv)4u2+8u
⇒ 4u(u+2)
Therefore, zeroes of polynomial equation 4u2 + 8u are (0, -2).
Sum of zeroes = 0+(-2) = -2 = -(8/4) = = -(Coefficient of u)/(Coefficient of u2)
Product of zeroes = 0×-2 = 0 = 0/4 = (Constant term)/(Coefficient of u2)
(v) t2–15
⇒ t2 = 15 or t = ±√15
Therefore, zeroes of polynomial equation t2 –15 are (√15, -√15)
Sum of zeroes =√15+(-√15) = 0= -(0/1)= -(Coefficient of t) / (Coefficient of t2)
Product of zeroes = √15×(-√15) = -15 = -15/1 = (Constant term) / (Coefficient of t2 )
(vi) 3x2–x–4
⇒ 3x2–4x+3x–4 = x(3x-4)+1(3x-4) = (3x – 4)(x + 1)
Therefore, zeroes of polynomial equation3x2 – x – 4 are (4/3, -1)
Sum of zeroes = (4/3)+(-1) = (1/3)= -(-1/3) = -(Coefficient of x) / (Coefficient of x2)
Product of zeroes=(4/3)×(-1) = (-4/3) = (Constant term) /(Coefficient of x2 )
2. Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively.
(i) 1/4 , -1
Solution:
From the formulas of sum and product of zeroes, we know,
Sum of zeroes = α+β = 1/4
Product of zeroes = α β = -1
∴ If α and β are zeroes of any quadratic polynomial, then the quadratic polynomial equation can be written as:
X2–(α+β)x +αβ = 0
X2–(1/4)x +(-1) = 0
4x2–x-4 = 0
Thus,4x2–x–4 is the quadratic polynomial.
(ii)√2, 1/3
Solution: Sum of zeroes = α + β =√2
Product of zeroes = α β = 1/3
∴ If α and β are zeroes of any quadratic polynomial, then the quadratic polynomial equation can be written as:
X2–(α+β)x +αβ = 0
X2 –(√2)x + (1/3) = 0
3x2-3√2x+1 = 0
Thus, 3x2-3√2x+1 is the quadratic polynomial.
(iii) 0, √5
Solution: Sum of zeroes = α+β = 0
Product of zeroes = α β = √5
∴ If α and β are zeroes of any quadratic polynomial, then the quadratic polynomial equation can be written as:
x2–(α+β)x +αβ = 0
x2–(0)x +√5= 0
Thus ,x2+√5 is the quadratic polynomial.
(iv)1, 1
Solution. Sum of zeroes = α+β = 1
Product of zeroes = α β = 1
∴ If α and β are zeroes of any quadratic polynomial, then the quadratic polynomial equation can be written as:
X2–(α+β)x +αβ = 0
X2–x+1 = 0
Thus , x2–x+1is the quadratic polynomial.
(v) -1/4, 1/4
Solution: Sum of zeroes = α+β = -1/4
Product of zeroes = α β = 1/4
∴ If α and β are zeroes of any quadratic polynomial, then the quadratic polynomial equation can be written as:
X2–(α+β)x +αβ = 0
X2–(-1/4)x +(1/4) = 0
4x2+x+1 = 0
Thus,4x2+x+1 is the quadratic polynomial.
(vi) 4, 1
Solution: Sum of zeroes = α+β =4
Product of zeroes = αβ = 1
∴ If α and β are zeroes of any quadratic polynomial, then the quadratic polynomial equation can be written as:
X2–(α+β)x+αβ = 0
X2–4x+1 = 0
Thus , x2–4x+1 is the quadratic polynomial.
Exercise 2.3
Question 1.) Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following:
(i) p(x) = x3-3x2+5x–3 , g(x) = x2–2
Solution: Dividend = p(x) = x3-3x2+5x–3
Divisor = g(x) = x2– 2
Quotient = x–3
Remainder = 7x–9
ii) p(x) = x4-3x2+4x+5 , g(x) = x2+1-x
Solution: Given,
Dividend = p(x) = x4 – 3x2 + 4x +5
Divisor = g(x) = x2 +1-x= x2-x+1
Quotient = x2 +x–3
Remainder = 8
(iii) p(x) =x4–5x+6, g(x) = 2–x2
Solution: Given,
Dividend = p(x) =x4 – 5x + 6 = x4 +0x2–5x+6
Divisor = g(x) = 2–x2 = –x2+2
Quotient = -x2-2
Remainder = -5x + 10
2. Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial:
(i) t2-3, 2t4 +3t3-2t2-9t-12
Solutions: Given,
First polynomial = t2-3
Second polynomial = 2t4 +3t3-2t2 -9t-12
As, the remainder is left as 0. Therefore, we say that, t2-3 is a factor of 2t4+3t3-2t2-9t-12.
(ii)x2+3x+1 , 3x4+5x3-7x2+2x+2
Solutions: Given,
First polynomial = x2+3x+1
Second polynomial = 3x4+5x3-7x2+2x+2
As , the remainder is left as 0. Therefore, we say that, x2 + 3x + 1 is a factor of 3x4+5x3-7x2+2x+2.
(iii) x3-3x+1, x5-4x3+x2+3x+1
Solutions: Given,
First polynomial = x3-3x+1
Second polynomial = x5-4x3+x2+3x+1
As, the remainder is not equal to 0. Therefore, we say that, x3-3x+1 is not a factor of x5-4x3+x2+3x+1 .
3. Obtain all other zeroes of 3x4+6x3-2x2-10x-5, if two of its zeroes are √(5/3) and – √(5/3).
Solutions: Since two zeroes are √(5/3) and -√(5/3) are the factors of polynomial f(x).
∴ (x –√(5/3)) (x+√(5/3) = x2-(5/3) = 0
(3x2−5)=0, is a factor of given polynomial f(x).
Now, when we will divide f(x) by (3x2−5) the quotient obtained will also be a factor of f(x) and the remainder will be 0.
Therefore, 3x4 +6x3 −2x2 −10x–5 = (3x2-5)(x2+2x+1)
Now, on further factorizing (x2+2x+1) we get,
X2+2x+1 = x2+x+x+1 = 0
x(x+1)+1(x+1) = 0
(x+1)(x+1) = 0
So, its zeroes are given by: x= −1 and x = −1.
Therefore, all four zeroes of given polynomial equation are:
√(5/3),- √(5/3) , −1 and −1.(Answer)
4. On dividing x3-3x2+x+2 by a polynomial g(x), the quotient and remainder were x–2 and –2x+4, respectively. Find g(x).
Solutions:Given,Dividend, p(x) = x3-3x2+x+2
Quotient = x-2
Remainder = –2x+4
To find the value of Divisor, g(x) =?
As we know,
Dividend = Divisor×Quotient + Remainder
∴ x3-3x2+x+2 = g(x)×(x-2)+(-2x+4)
X3-3x2+x+2-(-2x+4) = g(x)×(x-2)
X3-3x2+x+2+2x-4 = g(x) (x-2)
X3-3x2+3x-2=g(x) (x-2)
Now, for finding g(x) we will divide x3-3x2+3x-2 with (x-2)
Therefore, g(x) = (x2–x+1)
5. Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the division algorithm and
(i) deg p(x) = deg q(x)
(ii) deg q(x) = deg r(x)
(iii) deg r(x) = 0
Solutions: According to the division algorithm, dividend p(x) and divisor g(x) are two polynomials, where g(x)≠0. Then we can find the value of quotient q(x) and remainder r(x), with the help of below given formula;
Dividend = Divisor×Quotient+Remainder
∴ p(x) = g(x)×q(x)+r(x)
Where r(x) = 0 or degree of r(x)< degree of g(x).
Now let us proof the three given cases as per division algorithm by taking examples for each.
(i):deg p(x) = deg q(x)
Degree of dividend is equal to degree of quotient, only when the divisor is a constant term.
Let us take an example, 3x2+3x+3 is a polynomial to be divided by 3.
So, (3x2+3x+3)/3 = x2+x+1 = q(x)
Thus, you can see, the degree of quotient is equal to the degree of dividend.
Hence, division algorithm is satisfied here.
(ii)deg q(x) = deg r(x)
Let us take an example , p(x)=x2+x is a polynomial to be divided by g(x)=x.
So, (x2+x)/x = x+1 = q(x)
Also, remainder, r(x) = 0
Thus, you can see, the degree of quotient is equal to the degree of remainder.
Hence, division algorithm is satisfied here.
(iii)deg r(x) = 0
The degree of remainder is 0 only when the remainder left after division algorithm is constant.
Let us take an example, p(x) = x2+1 is a polynomial to be divided by g(x)=x.
So,( x2+1)/x= x=q(x)
And r(x)=1
Clearly, the degree of remainder here is 0.
Hence, division algorithm is satisfied here.
Exercise 2.4
1. Verify that the numbers given alongside of the cubic polynomials below are their zeroes. Also verify the relationship between the zeroes and the coefficients in each case:
(i) 2x3+x2-5x+2; -1/2, 1, -2
Solutions: Given, p(x) = 2x3+x2-5x+2
And zeroes for p(x) are = 1/2, 1, -2
∴ p(1/2) = 2(1/2)3+(1/2)2-5(1/2)+2 = (1/4)+(1/4)-(5/2)+2 = 0
p(1) = 2(1)3+(1)2-5(1)+2 = 0
p(-2) = 2(-2)3+(-2)2-5(-2)+2 = 0
Hence, proved 1/2, 1, -2 are the zeroes of 2x3+x2-5x+2.
Now, comparing the given polynomial with general expression, we get;
∴ ax3+bx2+cx+d = 2x3+x2-5x+2
a=2, b=1, c= -5 and d = 2
As we know, if α, β, γ are the zeroes of the cubic polynomial ax3+bx2+cx+d , then;
α +β+γ = –b/a
αβ+βγ+γα = c/a
α βγ = – d/a.
Therefore, putting the values of zeroes of the polynomial,
α+β+γ = ½+1+(-2) = -1/2 = –b/a
αβ+βγ+γα = (1/2×1)+(1 ×-2)+(-2×1/2) = -5/2 = c/a
α β γ = ½×1×(-2) = -2/2 = -d/a
Hence, the relationship between the zeroes and the coefficients are satisfied.
(ii) x3-4x2+5x-2 ;2, 1, 1
Solutions: Given, p(x) = x3-4x2+5x-2
And zeroes for p(x) are 2,1,1.
∴ p(2)= 23-4(2)2+5(2)-2 = 0
p(1) = 13-(4×12 )+(5×1)-2 = 0
Hence proved, 2, 1, 1 are the zeroes of x3-4x2+5x-2
Now, comparing the given polynomial with general expression, we get;
∴ ax3+bx2+cx+d = x3-4x2+5x-2
a = 1, b = -4, c = 5 and d = -2
As we know, if α, β, γ are the zeroes of the cubic polynomial ax3+bx2+cx+d , then;
α + β + γ = –b/a
αβ + βγ + γα = c/a
α β γ = – d/a.
Therefore, putting the values of zeroes of the polynomial,
α +β+γ = 2+1+1 = 4 = -(-4)/1 = –b/a
αβ+βγ+γα = 2×1+1×1+1×2 = 5 = 5/1= c/a
αβγ = 2×1×1 = 2 = -(-2)/1 = -d/a
Hence, the relationship between the zeroes and the coefficients are satisfied.
2. Find a cubic polynomial with the sum, sum of the product of its zeroes taken two at a time, and the product of its zeroes as 2, –7, –14 respectively.
Solutions: Let us consider the cubic polynomial is ax3+bx2+cx+d and the values of the zeroes of the polynomials be α, β, γ.
As per the given question,
α+β+γ = -b/a = 2/1
αβ +βγ+γα = c/a = -7/1
α βγ = -d/a = -14/1
Thus, from above three expressions we get the values of coefficient of polynomial.
a = 1, b = -2, c = -7, d = 14
Hence, the cubic polynomial is x3-2x2-7x+14
3. If the zeroes of the polynomial x3-3x2+x+1 are a – b, a, a + b, find a and b.
Solutions: Given, p(x) = x3-3x2+x+1
zeroes are given as a – b, a, a + b
Sum of zeroes = a – b + a + a + b
-b/a = 3a
-(-3)/1 = 3a
a=1
Thus, the zeroes are 1-b, 1, 1+b.
Now, product of zeroes = 1(1-b)(1+b)
-1/1 = 1-b2
Or , b2 = 1+1 = 2
b = √2
Hence, a=1 and b= √2 (answer).
4. If two zeroes of the polynomial x4-6x3-26x2+138x-35 are 2 ±√3, find other zeroes.
Solutions: Since this is a polynomial equation of degree 4, hence there will be total 4 roots.
Let f(x) = x4-6x3-26x2+138x-35
Since 2 +√3 and 2-√3 are zeroes of given polynomial f(x).
Let x= 2 ±√3
X-2 =±√3
Squaring on both sides,
X2-4x+4 = 3
X2-4x+1 = 0
X2-4x+1 is a factor of a given polynomial f(x).
Let us divide p(x) by X2-4x+1 to obtain other zeroes.
So, x4-6x3-26x2+138x-35 = (x2-4x+1)(x2 –2x−35)
Now, on further factorizing (x2–2x−35) we get,
X2–(7−5)x −35 = x2– 7x+5x+35 = 0
x(x −7)+5(x−7) = 0
(x+5)(x−7) = 0
So, its zeroes are given by:
x= −5 and x = 7.
Therefore, all four zeroes of given polynomial equation are: 2+√3 , 2-√3, −5 and 7.
5. If the polynomial x4-6x3+16x2- 25x+10 is divided by another polynomial x2-2x+k , the remainder comes out to be x+a , find k and a.
Solution: let us divide x4-6x3+16x2-25x+10 by
x2-2x+k.
Now, remainder = (2k-9)x-(8-k)k+10………..(1)
But remainder = x+a ( given )……………….(2)
From (1) and (2) , we get;
(2k-9)x-(8-k)k+10 = x+a
On comparing their coefficients, we have
2k-9 = 1
K= 5
And -(8-k)k+10 = a
a= -(8-5)5+10
Or, a = -3*5+10
Or, a = -15+10
Or, a = -5
Hence, K = 5 and a = -5 ( answer).







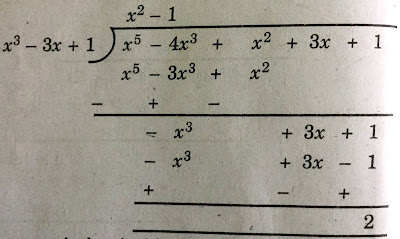



No comments:
Post a Comment
Comment for more details.....